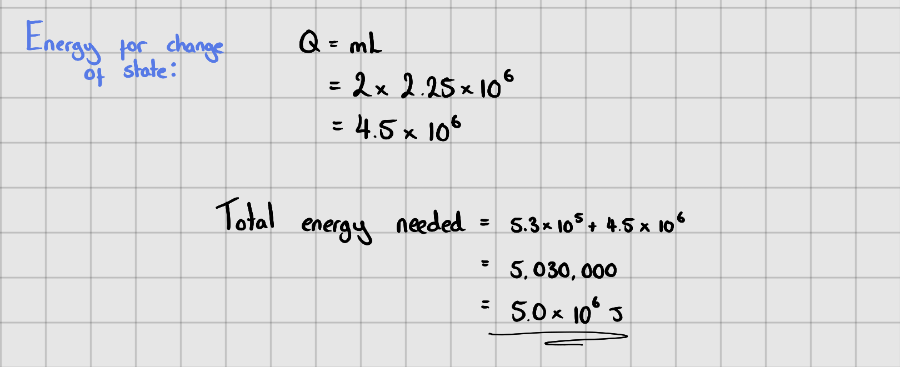Latent Heat Capacity

Equation

$$\LARGE{Q=mL}$$

Where,

$Q$ - Change in energy ($J$)

$m$ - Mass of substance ($kg$)

$L$ - Specific latent heat ($J\space kg^{-1}$)

Explanation

The specific latent heat of a substance is the amount of energy required to change the state of 1kg of the material.

Latent heat capacities can be split further into two distinct types of latent heat capacity:

Specific Latent Heat of Fusion - The work that must be done to convert 1 kg of a solid to a liquid
Specific Latent Heat of Vaporisation - The work that must be done to convert 1kg of a liquid to a gas

It is very important to understand that the latent heat capacity does not consider the potential change in temperature needed so the substance can actually change state. It only accounts for the energy needed to change the state. To work out the energy needed to be supplied/removed for the increase/decrease of temperature needed, one must use specific heat capacity.

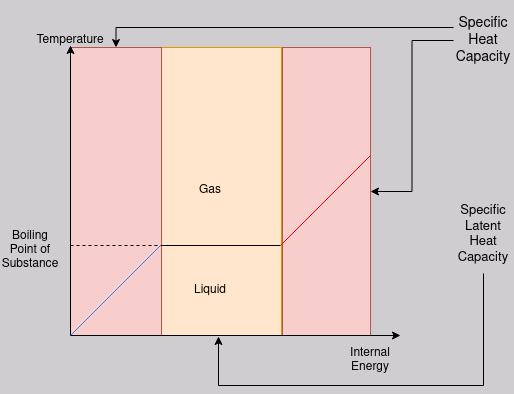
Below is the same graph as was in the Internal Energy notes, however this time it shows where the two types of heat capacities are ‘applicable’.

Since this graph shows the change of state between liquid and gas, you would have to use the latent heat of vaporisation.

Outside Of Specification Information

There are also specific latent heats of sublimation and deposition.

Remember that sublimation is where a solid transitions directly to a gas, bypassing the liquid phase, and deposition is where a gas transitions directly to a solid, also bypassing the liquid phase.

Examples of sublimation in nature:

Snow and Ice: Snow and ice undergo sublimation in dry and cold weather conditions.
Dry Ice: Dry ice is frozen carbon dioxide and undergoes sublimation at room temperature.
Iodine: Iodine crystals can undergo sublimation at room temperature, turning from a solid state into a gas.

Examples of deposition in nature:

Frost: Frost is formed when water vapor in the air undergoes deposition on a cold surface, such as grass or windows, forming ice crystals.
Clouds: Clouds are formed when water vapor in the air undergoes deposition on tiny particles, such as dust or salt, forming tiny ice crystals or droplets.

energy change in $J$energy change in $J$

Starter Questions

Latent Heat of Vaporisation of Water = $2.25 \times 10^{6} \space J\space {Kg}^{-1}$

$Q1$. Calculate the energy needed to change $2kg$ of liquid water to a gas, where the liquid is already at $100^{\circ}C$.

$Q2$. Calculate the energy needed to change $2kg$ of liquid water to a gas. The sample is at a starting temperature of $37^{\circ}C$.