3.1.1 - Periodicity

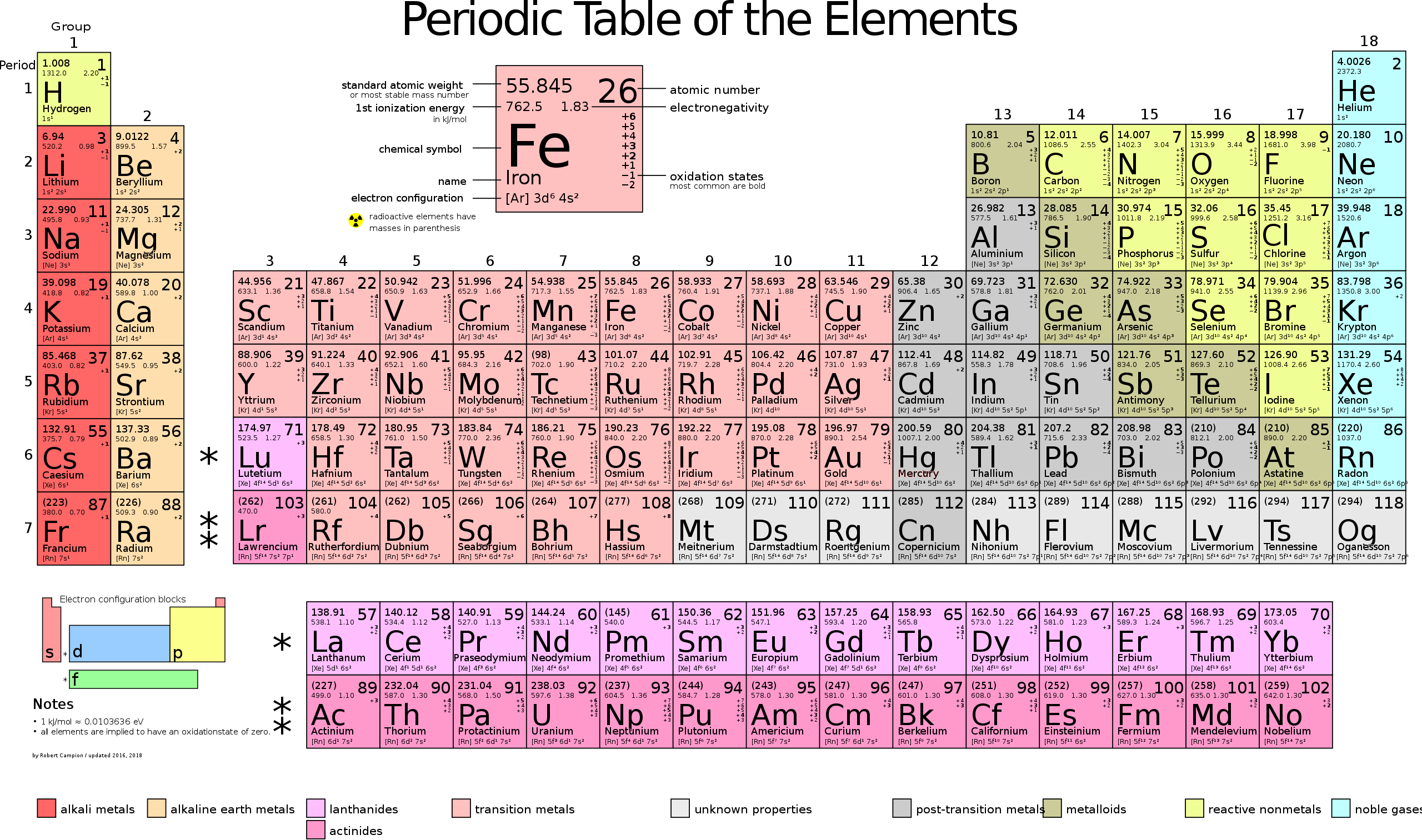
Structure of the Periodic Table

Throughout history, the structure of the Periodic table has changed, although not by much. Originally, a Russian chemist called Dmitri Mendeleev arranged known elements into different columns based on their chemical properties, and rows based on the intensity of the properties. For example, as you go down the rows, the elements in the first column, Group 1 elements, react more and more explosively with water.

Fast forward to modern times, and with a better understanding of the atom comes a new definition of the ordering of elements into what is called the Periodic Table.

The columns and rows are still very similar to Mendeleev’s original arrangement, but what they represent are now different:

• The column, or group, of an element now indicates the number of electrons occupying its atom’s highest occupied electron energy level. Since the properties of an element is determined by its electron affinity, elements in the same group have similar chemical properties.
• The row, or period, that an element’s in now indicates the highest occupied electron energy level in its atom. Since elements in a period are ordered left to right by group, the physical and chemical properties seen in each period show the same repeating trend.

These definitions are, however, only a by-product of the actual arrangement of the elements. They are now ordered by atomic number - the number of protons in their atoms’ nuclei - since this is the only consistent definition of an element.

All atoms with eight protons are oxygen atoms, and you can find oxygen isotopes and ions with different number of neutrons and electrons. This means that the number of protons defines the element, nothing else. The reason why we can still refer to number of electrons is simply because in an atom the numbers of protons and electrons are equal.

Ionisation Energy

Since atoms have the same number of electrons and protons, they are neutral and the charges are balanced. To upset this balance and remove one electrons requires some energy. This is known as the first ionisation energy:

The energy required to remove one mole of the most loosely held electrons from one mole of gaseous atoms to produce 1 mole of gaseous ions each with a charge of 1+.

$$ \text{Mg} _\text{(g)} \rightarrow \text{Mg} ^+ _\text{(g)} + \text{e} ^- $$

The second ionisation energy is the energy required to remove a second electron, and so on.

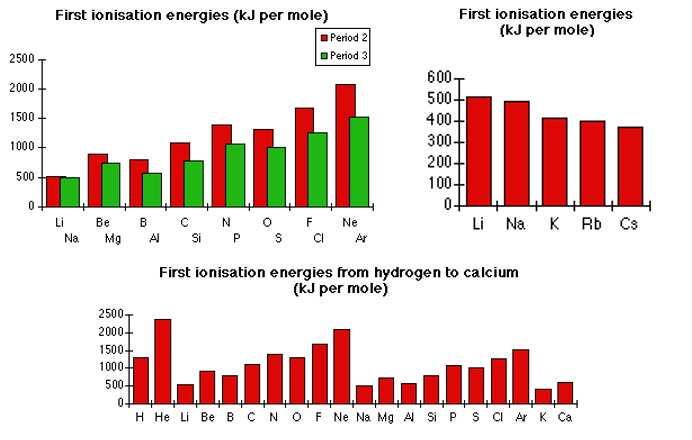
Below are three graphs of the first ionisation energies of various classifications of elements. The shapes of these graphs can be explained by the following factors:

NUCLEAR ATTRACTION:

As the period increases, so does the number of occupied electron energy levels. As each new level is occupied, the outer most electron is further away from the positively charged nucleus. This means the inward pull on the electron by the nucleus is weaker, and so less energy is required to ionise the atom. This is why period three elements appear to have a lower ionisation energy that period two elements (this is shown in graphs 1 and 2).

As well as whole energy levels, this is seen between different subshells also. In graphs 1 and 3, there are noticeable drops in ionisation energy between groups 2 & 3 and 5 & 6 elements. The drop between groups 2 & 3 is because the next electron is now in the p-subshell, which is slightly higher energy, so the attraction from the nucleus is less. The drop between groups 5 & 6 is because as the p-subshell is emptied, one from each orbital is removed, and then after the third one, emptying an incomplete orbital requires less energy than removing one of a pair.

ELECTRON SHIELDING:

As the period increases, so does the number of occupied electron energy levels. As each new level is occupied, the outer most electron is separated from the positively charged nucleus by more and more lower energy levels. The presence of negatively charged electrons between the inward pull and the outermost electron acts as an electrostatic ‘shield’, and so the outer electron is easier to remove (this is shown in graphs 1 and 2).

NUCLEAR CHARGE:

As the atomic number of an elements increase, the number of protons in the nucleus increases also. This means the nucleus gains a more and more positive charge as the period, and the group, increases. This means there is a greater attraction between the outermost electron and the nucleus in a period (same energy level) as the group increases. Therefore more energy is required to ionise the atoms (this is shown in graphs 1 and 3).

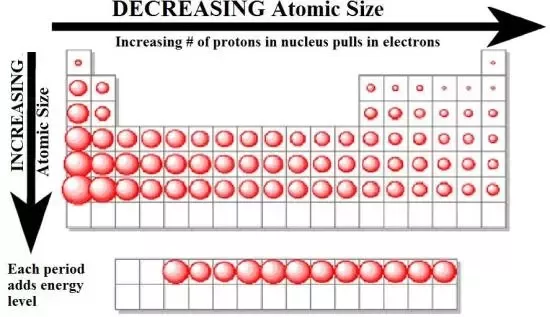
ATOMIC RADIUS:

As the number of electrons in an energy level increases, it gains a more negative charge. This leads to a greater attraction between the outer energy level and the positively charged nucleus, which pulls it closer. This means that the radius of an atom of an element in a period decreases as the group increases.

This decreases the space between the outermost electron and the nucleus, which in turn makes the attraction between the two greater. Therefore more energy is required to ionise the atoms (this is shown in graphs 1 and 3).

The diagram below shows the relationship between the position in the periodic table and the atomic radius:

Successive Ionisation Energies:

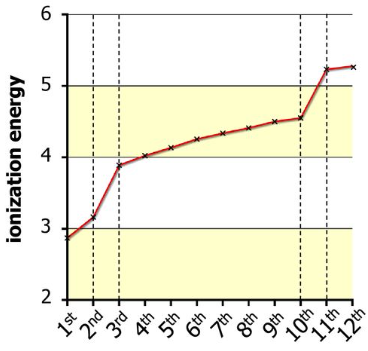
As mentioned above, the second ionisation energy is the energy required to remove a second electron from an ion with charge 1+. There exists an ionisation energy for every electron present in an atom as it is possible (while impractical) to remove every electron from an atom, leaving just its nucleus.

The graph below shows successive ionisation energies for magnesium, and clearly visible are two large jumps between the second and third energies, and the tenth and the eleventh:

These jumps exist because, after two or ten electrons have been removed, the next one is in the preceding principal energy level, so is closer to the nucleus. With the next electron being closer to the nucleus, a much larger amount energy is required to further ionise the 2+ ion or the 10+ ion.

Structure

In previous sections, it was shown that non-metals form covalent bonds with other non-metals and ionic bonds with metals. How, therefore, do metals bond with other metals?

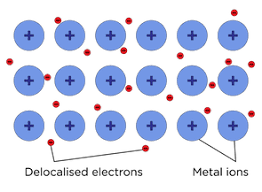
Metallic bonding is similar to ionic bonding, except all ions formed are cations since they are all metal ions. Stopping them from repelling each other and the metal atomising is a sea of delocalised electrons originally part of the metal atoms. This ‘sea’ runs between all the metal cations, acting like electrostatic glue.

The definition of a metallic bond is therefore:

The electrostatic force of attraction between positive metal cations and a sea of delocalised electrons.

This produces a giant metallic lattice, similar to an ionic lattice, of metal cations. Because of the presence of free electrons, metals can conduct electricity when solid; whereas ionic lattices cannot due to the static nature of oppositely charged ions in the solid. Ionic compounds can conduct when in solution because the ions are free to move, but metals are not soluble in water, so only conduct in solid, liquid and gas forms.

GIANT VS SIMPLE STRUCTURE:

A giant structure, as in metallic and ionic bonding, is a repeating pattern of atoms or ions bonded in a solid. In metallic and ionic lattices, the ions form a seemingly never-ending array of ions, and so is giant.

A simple structure, as in the majority of covalent substances, is a number of single particles held together by intermolecular forces. In water for example, individual water molecules are not fully bonded together, but are held together by the interaction between the partially positive hydrogen and partially negative oxygen. While this is called a hydrogen ‘bond’, it is strictly not a proper bond.

There are, however, some covalent substances that form giant structures. These elements are called the metalloids, as they shared some properties with metals, and yet form giant covalent crystals. As well as metalloids, carbon is unique as it is the only proper non-metal that forms a giant covalent structure.

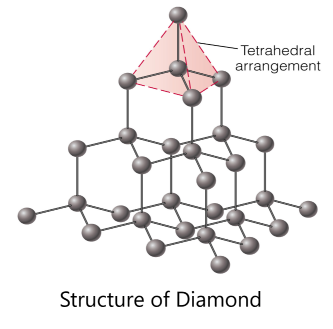
Carbon forms three different allotropes - unique giant structures - and they are diamond, graphene and graphite. In diamond, each carbon atom bonds to four other carbons in a tetrahedral shape. This means it has no free electrons that can move. Therefore diamond does not conduct electricity.

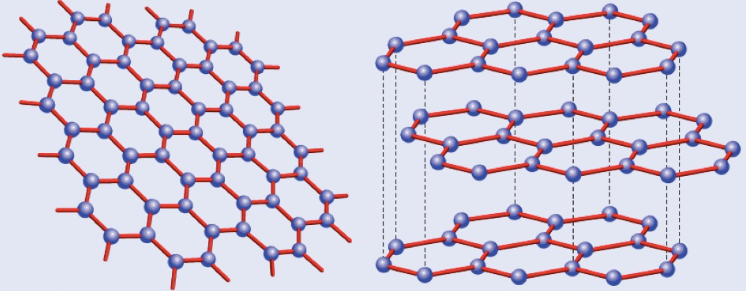
In graphene, each carbon atom bonds to three other carbons in a trigonal planar shape. This leaves one electron free to move, and so can conduct electricity. Multiple graphene sheets stacked upon each other is called graphite, and are held together by weak intermolecular forces. This means that while each sheet is very strong, they can easily move over each other and break away.

Properties of Giant Structures

In a giant structure, each molecule, atom or ion is head by a strong electrostatic force to multiple others. This gives the macrostructure (what we can see with our own eyes) certain properties.

For example, in a giant metallic structure, all ions are the same size, and so can the layers can slide over each other. This is what makes metals malleable.

Conversely, in a giant ionic lattice, the cations and anions are likely not to be the same size, and so the layers cannot slide over each other. This is why salts are quite brittle, because the locked structure of the lattice keeps it from breaking, up to a point, where there is enough pressure to cause the layers to eventually move, placing anions next to other anions. This causes the whole structure to break due to the repulsion.

In a carbon or metalloid giant structure, the covalent bonds - which are the strongest type of bond - require an incredible amount of energy to break. This results in very high melting and boiling points, insolubility in water, and very strong but brittle crystals.