Nuclear Radius and Density

Nuclear Radius

We have now discussed how we go about measuring / approximating the radius of an atomic nucleus.

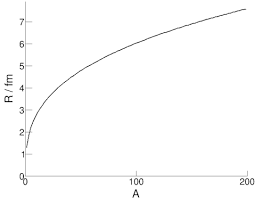
If we collect information on the radii of different nuclei, we can create a graph of nuclear radius ($R$) against nucleon number ($A$):

It is clear to see this shows an exponential fashion of growth. This suggests it may show a linear correlation when plotted on a log graph, and indeed it does:

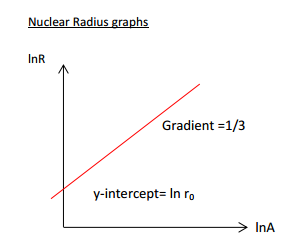
Those readers who take / have got sufficiently far into A-Level Maths will know that a log graph (a graph where the quantities on both axes are logged) can be written as follows:

$$ log \; A = m \; log \; B + log \; c $$

Applied to the context of the graph above, we get:

$$ ln \; R = \frac{1}{3} \; ln \; A + ln \; R_{0} $$

The gradient being $\frac{1}{3}$ is found by simply analysing the graph. Furthermore, the y-intercept ($R_{0}$) is known to be roughly $1.4 \times 10^{-15} \space m$ or 1.4 femtometres.

Using the laws of logarithms, let us rearrange the equation above:

$$ \begin{aligned} ln \; R &= ln \; A^{\frac{1}{3}} + ln \; R_{0}\\\ ln \; R &= ln(R_{0}A^{\frac{1}{3}})\\\ e^{ln \; R} &= e^{ln(R_{0}A^{\frac{1}{3}})}\\\ R &= R_{0}A^{\frac{1}{3}}\end{aligned} $$

As you can see, this gives us the final equation of:

$$ \LARGE{R = R_{0}A^{\frac{1}{3}}} $$

Where,

$R$ - The radius of the nucleus

$A$ - The nucleon number of the nucleus

$R_0$ - 1.4fm (see more information at the end of this page)

Nuclear Density

Now we have a generalised equation for the expected radius of any atomic nucleus, we can find a generalised equation for density. Let us try this:

$$ \large{\begin{aligned} \rho &= \frac{m}{v}\\\ \rho &= \frac{A \times m_\text{nucleon}}{\frac{4}{3} \pi R^3}\\\ \rho &= \frac{A \times m_\text{nucleon}}{\frac{4}{3} \pi (R_0 A^\frac{1}{3})^3}\\\ \rho &= \frac{3 \times m_\text{nucleon}}{4\pi R_0^3} \end{aligned}} $$

The alert reader will quickly notice that this final equation is constituted by only constants, and will realise this leads to the conclusion that the nuclear density is the same in all nuclei, no matter the element them make up!

If you substitute the values of the constants used in the density equation, you get a value of —

$$ \LARGE{\rho = 1.45 \times 10^{17} kg \; m^{-3}} $$

To give you an idea of exactly how dense nuclear matter is, let us approximate the weight of a shot glass if we filled its full volume with nuclear matter:

We’ll assume the shot glass has a volume of $44ml$ or $4.4 \times 10^{-5}$.

$$ \begin{aligned} \rho &= \frac{mass}{volume}\\\ mass &= \rho \times volume\\\ &= 1.45 \times 10^{17} \times 4.4 \times 10^{-5} \\\ &= 6.38 \times 10^{12}kg\end{aligned} $$

That’s a pretty heavy shot!

What is $R_0$?

Many sources fail to explain intuitively what $R_0$ really is so I want to cover it here.

Let us look back at the previous graph:

We can see that $ln R_{0}$ is the y-intercept. Therefore, it is the value of the equation when $ln \; A = 0$. This is not the same as when $A$ is 0:

$$ \begin{aligned}ln \\\; A &= 0\\\ A &= e^{0}\\\ A &= 1\end{aligned} $$

It is, in fact, the value that is measured when there is a nucleon number of 1; it is the radius of a single nucleon!! Therefore, you can think of $R_{0}$ as the radius of a neutron or proton.

Another way of looking at this is by considering $R_0$ as the radius of a nucleon to begin with and considering how this would be used to find the radius of the nucleus as a whole:

The volume of each nucleon - if we take it to be spherical and have a radius $R_0$ - would be:

$$ V_\text{nucleon} = \frac{4}{3} \pi R_0^3 $$

Therefore, for a nucleus with atomic number A, the volume would be

$$ V_\text{nucleus} = A \times \frac{4}{3} \pi R_0^3 $$

If we say the nucleus has radius $R$, we can rewrite this as:

$$ \frac{4}{3} \pi R^3 = A \times \frac{4}{3} \pi R_0^3 $$

Which cancels to give:

$$ \large{R = R_0 A^\frac{1}{3}} $$

I hope this shows an intuitive way of understanding the value of R_0.