Nuclear Radius by Electron Diffraction

Thanks to the fact that an electron exhibits a wave-particle duality and is a lepton (so does not interact with the atomic nucleus through the strong interaction), electron diffraction is a much more accurate method of determining the radius of a nucleus.

Remember the De Broglie wavelength equation from the Quantum Phenomena section: $\lambda = \frac{h}{mv}$. For electron diffraction to occur in a manner suitable for determining the radius of an atomic nuclei, the electrons must be travelling at very high speeds. At such speeds, Einstein’s Theory of Special Relativity comes into play, and changes how we can define velocity, distance, and time itself. Unless you are taking the AQA ‘Turning Points In Physics’ option, you will not study this topic in the AQA A-Level course. For this reason, I do not give the derivation of the following formula:

For a particle at speeds close to the speed of light (so-called ‘relativistic particles’), the De Broglie wavelength is approximately:

$$ \large{\lambda \simeq \frac{hc}{E}} $$

Where $E$ is the energy of the particle in Joules.

The wavelength of the electron must be very small (approx. $10^{-15}m$ ) and so the beam of electrons must have very high energy. Each electron diffracts off an individual nucleus in a somewhat similar way to that which is shown below (¹):

The resulting pattern of minima and maxima is dependent on the De Broglie wavelength and the radius of the nucleus.

The first minimum in the diffraction pattern appears where:

$$ \LARGE{\sin{\theta} \simeq \frac{1.22\lambda}{d}} $$

Where $d$ is the diameter of the nucleus the electrons have been diffracted by.

Therefore,

$$ \LARGE{\sin{\theta} \simeq \frac{0.61\lambda}{R}} $$

Where,

$\theta$ - the diffraction angle at which the first minimum is found.

$\lambda$ - De Broglie wavelength of the electrons.

$R$ - the radius of the nucleus the electrons have been diffracted by.

²

History

I did not cover the development of this method in my historic account at the beginning of this chapter, and so I would like to take some time to briefly (as I think is so useful for furthering one’s understanding of the subject) to put the Physics in its historical context. - This will eventually migrate to the Quantum Phenomena section when it is created, since it is more applicable there.

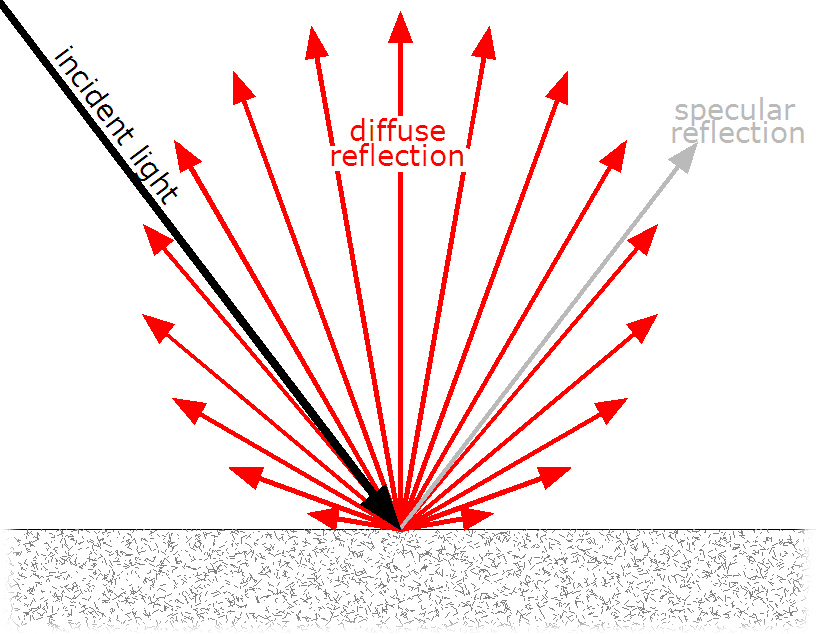
It was 1927 when American Physicists Clinton Davisson and Lester Germer were measuring the angles that electrons would bounce off at when a beam of said leptons were shot at a nickel crystal. The crystal was polycrystalline which meant, since its structure consists of many microscopic crystals bonded together and randomly oriented, that the beam reflected diffusely.

For a beam to reflect diffusely is to be reflected in many angles. It is what happens when light reflects of a rough surface; there is not one point to which all light is reflected. This is shown below (Image from: Д.Ильин, ³):

At some point in the experiment, there was a leak in the vacuum chamber and air promptly entered. The nickel reacted with the air and an oxide layer formed on the sample. Trying to remove this, the two scientists heated the sample up to very close to its boiling point. This, initially unbeknown to them, had the effect or orienting the microscopic crystals to the same plane; the surface now acted (from the perspective of the electron) as one single crystal.

When the experiment was then continued, the results were majorly different. Instead of a smooth variation of the number of electrons detected at all angles (due to the diffuse reflection) it was observed that at certain angles, there were maxima - the reflection had become less ‘perfectly diffuse’. The pattern that emerged was very similar to that of X-ray diffraction and was the first direct experimental confirmation of De Broglie’s wave-particle hypothesis.