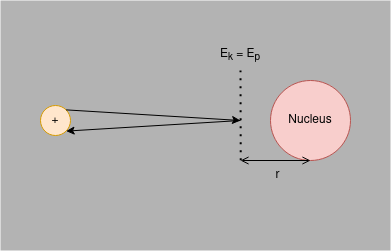
Measuring the Radius of an Atomic Nucleus by Closest Approach

The nucleus of an atom is positively charged and so has an electric field. To move a positively charged particle towards an atomic nucleus, therefore, requires work to be done by the particle. Energy must be changed from the particle’s kinetic energy ($E_{K}$) store to overcome the increasing repulsion due to the electric field; kinetic energy is transferred to electric potential energy ($E_{P}$).

There is, therefore, a point where a positively charged particle that is approaching an atomic nucleus with some initial velocity would stop, before accelerating away from the nucleus.

If you assume that charge in the nucleus is evenly distributed then inductively assume that you can model all the charge as being concentrated in the centre of the nucleus - a centre of charge. Therefore, the distance at which $E_{K} = E_{P}$ (denoted $r$ in the diagram) can be an approximation of the radius of the nucleus. It should be noted, however, that it is not a particularly good approximation; it gives only the maximum radius the nucleus could be.

At greater initial velocities, the particle will have more $E_{K}$ and so be able to get a lower value for $r$; the quicker the approach velocity of the particle relative to the nucleus, the more accurate the approximation for the radius of said nucleus will be.

Equation

$$ \large{ \begin{aligned} E_{K} &= E_{P} \\\ \frac{1}{2}mv^{2} &= \frac{1}{4\pi \epsilon_{0}} \frac{Q_{particle} Q_{nucleus}}{r}\\\ r &= \frac{2}{4\pi \epsilon_{0}}\frac{Q_{particle} Q_{nucleus}}{mv^{2}} \end{aligned} } $$

Where,

$r$ - the distance of closest approach of particle to nucleus (approximation for radius of nucleus)

$\epsilon_{0}$ - the permittivity of free space

$Q_{particle}$ and $Q_{nucleus}$ - the charge on the particle and nucleus, respectively

$m$ - mass of the particle approaching the nucleus

$v$ - the velocity of the particle approaching the nucleus

You will most likely not use this equation for $r$, since you may find it easier to work with $E_{K}$ as a numerical value and dividing through by that number (e.g. $10 \times 10^{-13}J$). Understanding the derivation for $r$ above, however, will help you understand what you are acheiving by rearranging numerically for $r$.

Starter Questions

Coming Soon