2.2.1 - Electron Structure

Hierarchy of Electron Arrangement

In an atom, the electrons orbit the nucleus, but unlike the orbits of the planets around the sun, the path an electron takes is not defined. Instead, they spin around the nucleus randomly.

ELECTRON ENERGY LEVELS

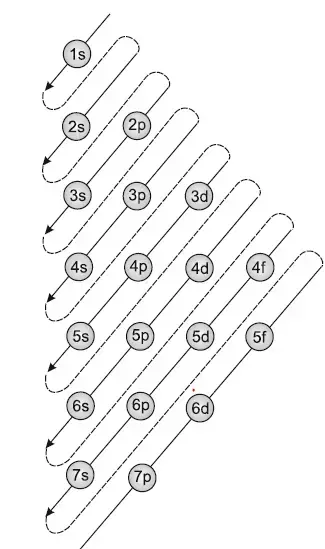
Electrons are arranged primarily in energy levels, the outermost occupied of which is denoted by the period (row) that an element resides in the periodic table. All atoms have 7 electron energy levels, but those in earlier periods have empty energy levels. Electrons gradually fill the energy levels from lowest to highest.

SUB-SHELLS

Each electron energy level can be divided into subshells, which contain different number of electrons. There are four types of subshells:

• s-subshells contain up to 2 electrons, and has the lowest energy level in each full electron energy level
• p-subshells contain up to 6 electrons
• d-subshells contain up to 10 electrons
• f-subshells contain up to 14 electrons, and has the highest energy level in each full electron energy level

Electrons gradually fill the subshells from lowest to highest energy level, and across the groups of the periodic table.

The above diagram shows the subshells found in each energy level, as well as the Aufbau Principle. The Aufbau Principle determines the order in which subshells are filled by following the arrows. The reason it is perhaps different from what is expected is because the 4p subshell required less energy to fill than the 3d subshells. However, on emptying, the 3d subshell does not empty first. This is because once the 4s subshell has been filled, it increases in energy level, so empties first.

All this leads to an updated notation for electronic configuration. The notation is made up of the electron energy level, the type of orbital and the number of electrons in it:

$$ \huge1\text{s}^2 $$

means the s-orbital of the first electron energy shell contains 2 electrons.

Further to this:

$$ \huge\text{1s}^2\text{2s}^2\text{2p}^5 $$

means that 2 electrons occupy the s-orbital of the first electron energy level, 2 more occupy the s-orbital in the second energy level and 5 more occupy the p-subshell of the second energy level.

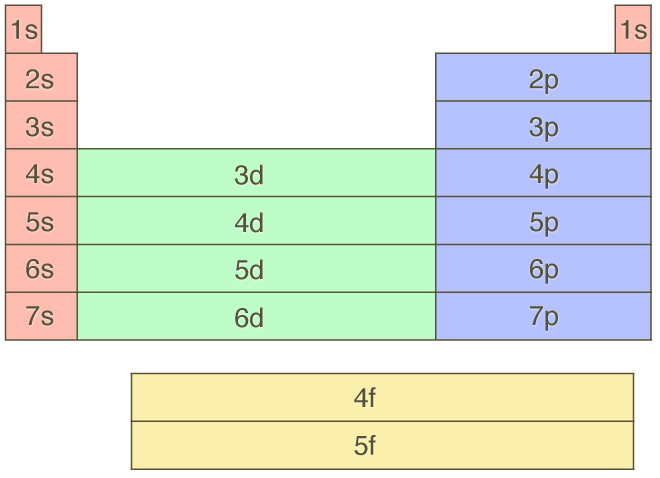
It also means that the periodic table can be divided into blocks. The s-block comprises all the elements whose outermost electrons occupy an s-subshell. Similarly, elements in the p-block have outermost electrons in a p-subshell, and so on. The diagram below shows the exact subshell in which the outermost electron occupies, and colour-codes the different blocks.

ORBITALS

Subshells can be further divided into individual electron orbitals. This is the smallest subunit of electronic arrangement.

An orbital is defined as:

A region around the nucleus that can hold up to two electrons, with opposite spins.

which means an s-subshell is made up of one orbital, a p-subshell is made up of three orbitals, d-subshells are five orbitals and f-subshells are seven.

Note - spin (also encountered in NMR spectroscopy) is a quantum property of subatomic particles - it does not mean that the electrons are spinning. For this course, understanding of spin is not required, but knowledge that the two electrons in an orbital have opposite spin - up and down - is.

When orbitals fill with electrons, those of equal energy level occupy singly before pairing. For example, a p-subshell fills like this:

1. Electron with up-spin occupies the first p-orbital
2. Electron with up-spin occupies the second p-orbital
3. Electron with up-spin occupies the third p-orbital
4. Electron with down-spin occupies the first p-orbital, filling the orbital
5. Electron with down-spin occupies the second p-orbital, filling the orbital
6. Electron with down-spin occupies the third p-orbital, filling the orbital

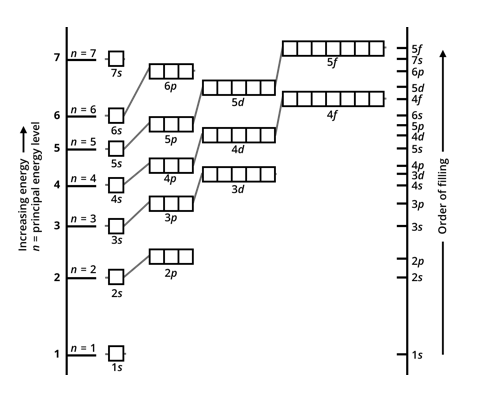
This is represented by a model called ‘electrons in box representation’, in which orbitals (boxes grouped into subshells are shown in a graph, with the y-axis being the energy level. The diagram below is an empty electron-in-box diagram, and shows the order of filling.

Note - this diagram omits the 7p subshell and orbitals

A partially filled d-subshell may look like this:

$$ \boxed{\upharpoonleft \downharpoonright}\boxed{\upharpoonleft \downharpoonright}\boxed{\upharpoonleft \\\: \thinspace}\boxed{\upharpoonleft \\\: \thinspace}\boxed{\upharpoonleft \\\: \thinspace} $$

with each single-headed arrow representing an electron, and its direction indicating the electron’s spin.

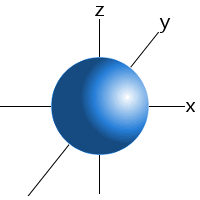
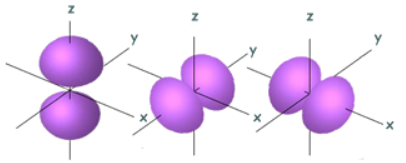
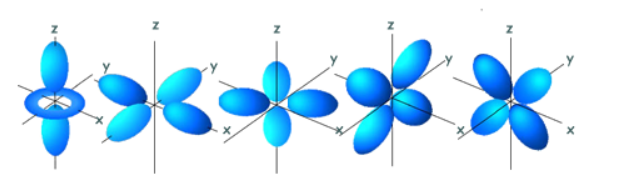
Finally, each type of orbital has a specific 3D shape. This shape represents the region around the nucleus where the electron occupying that orbital is 95% likely to be. The name of the orbitals are actually derived from their shapes:

• s-orbital: sphere

• p-orbitals: propeller (although more commonly referred to as dumbbell-shaped now)

• d-orbitals: doughnut

• f-orbitals: flower

Electronic Configuration

Using all these rules for electron arrangement, it is possible to identify each element by their unique electronic configuration. The signature part of an element’s electronic configuration is the very last part. For example, if the last part was 5p$\small^4$, then using the block diagram above, we can place it in the p-block (blue), in the 5th row (5p), and finally pin-point it as the 4th element, which would be tellurium.

But the convention is to show the entire electron structure, so we indicate that every subshell before 5p is full. Using the Aufbau Principle, we can identify which subshells these are, and write them in order, filling them with the number of electrons they can possibly carry:

$$ 1\text{s}^22\text{s}^22\text{p}^63\text{s}^23\text{p}^64\text{s}^23\text{d}^{10}4\text{p}^65\text{s}^24\text{d}^{10}5\text{p}^4 $$

This also gives information on the total number of electrons, and by extension protons, in the atom.

Another convention for shown electronic configuration is to use the noble gases as shorthand. Noble gases are in group 8 of the periodic table, and so every energy level, subshell and orbital is completely full. This is why they are so unreactive.

Therefore instead of writing 1s$\small^{2}$2s$\small^{2}$2p$\small^{6}$3s$\small^{2}$3p$\small^{6}$4s$\small^{2}$3d$\small^{10}$4p$\small^{6}$, which is the configuration for Krypton (Kr), we can symbolise it with [Kr]. This makes a second configuration for tellurium:

$$ \text{[Kr]}5\text{s}^24\text{d}^{10}5\text{p}^4 $$

As for ions, metals lose electrons and non-metals gain electrons to form them. Ions usually form to fill or empty an orbital or subshell, but the way that subshells empty is not the reverse of the way they fill up. As mentioned previously, 4s fills and empties before 3d because of the way the energy levels change. Metals in the s-, d- and f-blocks lose from the s orbitals first, which is why most of them form 2+ ions (group one elements don’t because they only have to lose one electron). Metals in the p-block lose from the p-subshell first, and then sometimes from the s-subshell as well, which is why bismuth can form 3+ ions, losing only from its 6p-subshell; and 5+ ions, losing from both its 6p and 6s subshells.

Knowing this, the electronic configuration of a Magnesium 2+ ion is therefore:

$$ 1\text{s}^22\text{s}^22\text{p}^6 $$

having lost both electrons from its 3s subshell. Notice that this is also the electronic configuration of an atom of Neon, so could be written as just [Ne].