2.1.1 - Atomic Structure and Isotopes
Atomic Structure
The atom is the smallest uniquely-determined unit of mass. In the most widely accepted model, each atom has a dense centre, the nucleus, and orbiting around it are electrons.
In the nucleus, there exist two types of subatomic particles (nucleons):
- Neutrons
- Neutral charge
- Relative atomic mass of 1
- Determine the isotope
- Protons
- Positive charge of +1
- Relative atomic mass of 1
- Determine the element
As above, orbiting the nucleus are electrons, with a negative charge of -1 and relative atomic mass of . The number of electrons compared with protons determines the ionic charge and oxidative state of an atom.
The relative atomic mass of an atom is the sum of the masses of neutrons and protons (electrons have negligible mass). It may also be shown as .
Isotopes
While the number of protons determines the element that an atom is, the number of neutrons can vary without affecting most of the properties of the atom. Atoms with the same number of protons but different numbers of neutrons are known as isotopes. It is important to note that while any number of isotopes is possible, some are more stable than others, so are more prevalent in nature.
Isotopes can be denoted in multiple ways. For example, an atom with 6 protons and 6 neutrons is carbon, and its total A is 12. This is written as carbon-12, C-12, C or C. Similarly, an atom with 6 protons and 7 neutrons is still carbon, as it has 6 protons, but its A is 13. Therefore it is carbon-13, C-13, C or C.
Relative Mass
When determining relative mass, the actual mass of an atom in not taken into account. Any relative mass is in comparison with the mass of the nucleons in a carbon-12 isotope. Since there are 12 nucleons in a C-12 isotope, it is one twelfth the mass of the isotope itself.
Relative Atomic Mass:
The weighted mean mass of atoms of an element compared with one twelfth the mass of a carbon-12 isotope.
Relative Isotopic Mass:
The mass of an isotope of an element compared with one twelfth the mass of a carbon-12 isotope.
To calculate the relative atomic mass, a weighted mean is taken of all stable isotopes in a sample. A weighted mean is calculated similarly to an ordinary mean, but each relative isotopic mass is multiplied by its relative abundance as a percentage, then the sum is divided by 100.
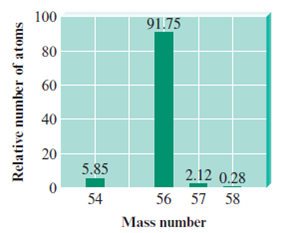
For example, a sample of iron contains four isotopes. In the table are the isotopic masses and relative abundances of these isotopes:
| Isotope | Relative Isotopic Mass | Relative Abundance |
|---|---|---|
| Iron-54 | 54 | 5.75% |
| Iron-56 | 56 | 91.75% |
| Iron-57 | 57 | 2.12% |
| Iron-58 | 58 | 0.28% |
For this sample, the relative atomic mass is calculated using the equation:
While the value obtained was actually 55.8558, A values are given to one decimal place.
Measuring Isotopes
In order to find the isotopic masses and their relative abundances, a piece of equipment is used that detects the mass of ions. It is called a mass spectrometer and is comprised of a tube with a 90 turn in it. First, an electron is knocked from the sample, forming an ion, and then it is fired along the tube. An electromagnetic sits at the inside of the corner, ‘pulling’ the ions around it. The more massive an ion is, the less effect the magnet has, so it collides with the tube earlier.
The result is a stick graph with values equating to the isotopic mass on the x-axis, and the relative abundance on the y-axis.
Above is the mass spectrum of the sample of iron. While the number on the x-axis is equal to the mass, the units are instead of . It is important to note that in an exam, the distinction must be made, in that 56 implies 56 .